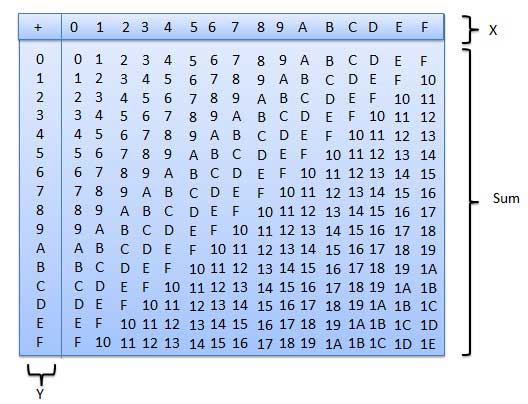
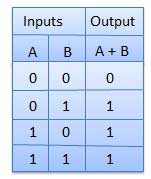
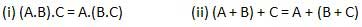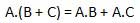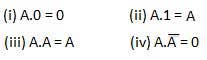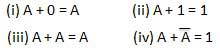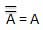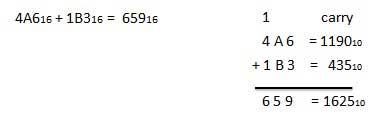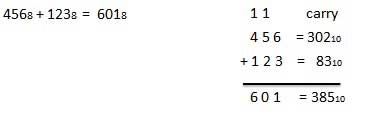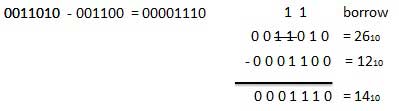Logic Gates

---

Logic gates are the basic building blocks of any digital system. It is an electronic circuit having one or more than one input and only one output. The relationship between the input and the output is based on a certain logic. Based on this, logic gates are named as AND gate, OR gate, NOT gate etc.

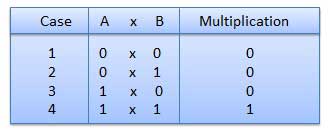
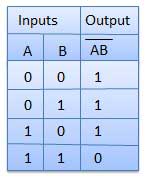
AND Gate

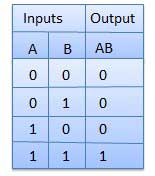
A circuit which performs an AND operation is shown in figure. It has n input (n >= 2) and one output.

Logic diagram

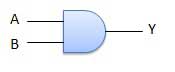
Truth Table

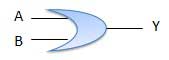
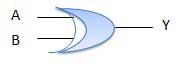
OR Gate

A circuit which performs an OR operation is shown in figure. It has n input (n >= 2) and one output.

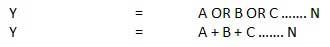
Logic diagram

Truth Table

NOT Gate

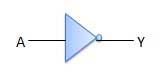
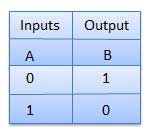
NOT gate is also known as Inverter. It has one input A and one output Y.

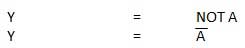
Logic diagram

Truth Table

NAND Gate

A NOT-AND operation is known as NAND operation. It has n input (n >= 2) and one output.

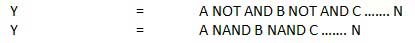
Logic diagram

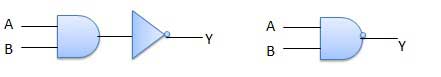
Truth Table

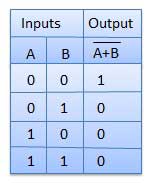
NOR Gate

A NOT-OR operation is known as NOR operation. It has n input (n >= 2) and one output.

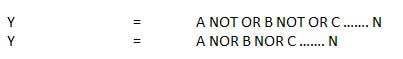
Logic diagram

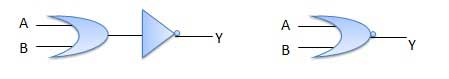
Truth Table

XOR Gate

XOR or Ex-OR gate is a special type of gate. It can be used in the half adder, full adder and subtractor. The exclusive-OR gate is abbreviated as EX-OR gate or sometime as X-OR gate. It has n input (n >= 2) and one output.

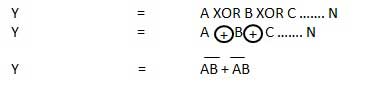
Logic diagram

Truth Table

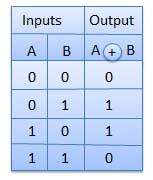
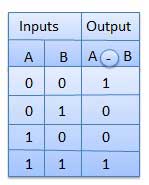
XNOR Gate

XNOR gate is a special type of gate. It can be used in the half adder, full adder and subtractor. The exclusive-NOR gate is abbreviated as EX-NOR gate or sometime as X-NOR gate. It has n input (n >= 2) and one output.

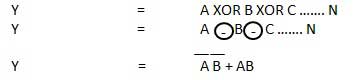
Logic diagram

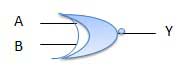
Truth Table

Boolean Algebra

---

Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It uses only the binary numbers i.e. 0 and 1. It is also called as Binary Algebraor logical Algebra. Boolean algebra was invented by George Boole in 1854.

Rule in Boolean Algebra

Following are the important rules used in Boolean algebra.

• Variable used can have only two values. Binary 1 for HIGH and Binary 0 for LOW.

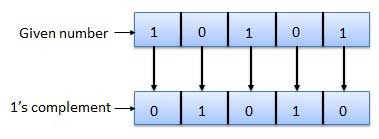
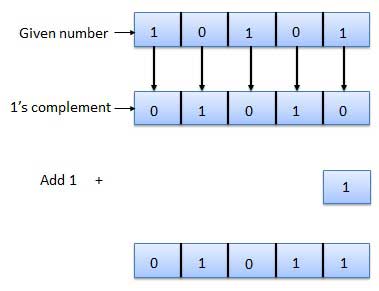
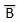• Complement of a variable is represented by an overbar (-). Thus, complement of variable B is represented as . Thus if B = 0 then = 1 and B = 1 then  = 0.

• ORing of the variables is represented by a plus (+) sign between them. For example ORing of A, B, C is represented as A + B + C.

• Logical ANDing of the two or more variable is represented by writing a dot between them such as A.B.C. Sometime the dot may be omitted like ABC.

Boolean Laws

There are six types of Boolean Laws.

Commutative law

Any binary operation which satisfies the following expression is referred to as commutative operation.

Commutative law states that changing the sequence of the variables does not have any effect on the output of a logic circuit.

Associative law

This law states that the order in which the logic operations are performed is irrelevant as their effect is the same.

Distributive law

Distributive law states the following condition.

AND law

These laws use the AND operation. Therefore they are called as AND laws.

OR law

These laws use the OR operation. Therefore they are called as OR laws.

INVERSION law

This law uses the NOT operation. The inversion law states that double inversion of a variable results in the original variable itself.

Important Boolean Theorems

Following are few important boolean Theorems.

Boolean function/theorems	Description
Boolean Functions	Boolean Functions and Expressions, K-Map and NAND Gates realization
De Morgan's Theorems	De Morgan's Theorem 1 and Theorem 2

Hexadecimal Arithmetic

---

Hexadecimal Number System

Following are the characteristics of a hexadecimal number system.

• Uses 10 digits and 6 letters, 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.

• Letters represents numbers starting from 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.

• Also called base 16 number system.

• Each position in a hexadecimal number represents a 0 power of the base (16). Example − 16⁰

• Last position in a hexadecimal number represents an x power of the base (16). Example − 16^x where x represents the last position - 1.

Example

Hexadecimal Number − 19FDE₁₆

Calculating Decimal Equivalent −

Step	Binary Number	Decimal Number
Step 1	19FDE16	((1 × 164) + (9 × 163) + (F × 162) + (D × 161) + (E × 160))10
Step 2	19FDE16	((1 × 164) + (9 × 163) + (15 × 162) + (13 × 161) + (14 × 160))10
Step 3	19FDE16	(65536 + 36864 + 3840 + 208 + 14)10
Step 4	19FDE16	10646210

Note − 19FDE₁₆ is normally written as 19FDE.

Hexadecimal Addition

Following hexadecimal addition table will help you greatly to handle Hexadecimal addition.

To use this table, simply follow the directions used in this example − Add A₁₆and 5₁₆. Locate A in the X column then locate the 5 in the Y column. The point in 'sum' area where these two columns intersect is the sum of two numbers.

A16 + 516 = F16. 

Example − Addition

Hexadecimal Subtraction

The subtraction of hexadecimal numbers follow the same rules as the subtraction of numbers in any other number system. The only variation is in borrowed number. In the decimal system, you borrow a group of 10₁₀. In the binary system, you borrow a group of 2₁₀. In the hexadecimal system you borrow a group of 16₁₀.

Example - Subtraction

Octal Arithmetic

---

Octal Number System

Following are the characteristics of an octal number system.

• Uses eight digits, 0,1,2,3,4,5,6,7.

• Also called base 8 number system.

• Each position in an octal number represents a 0 power of the base (8). Example: 8⁰

• Last position in an octal number represents an x power of the base (8). Example: 8^x where x represents the last position - 1.

Example

Octal Number − 12570₈

Calculating Decimal Equivalent −

Step	Octal Number	Decimal Number
Step 1	125708	((1 × 84) + (2 × 83) + (5 × 82) + (7 × 81) + (0 × 80))10
Step 2	125708	(4096 + 1024 + 320 + 56 + 0)10
Step 3	125708	549610

Note − 12570₈ is normally written as 12570.

Octal Addition

Following octal addition table will help you to handle octal addition.

To use this table, simply follow the directions used in this example: Add 6₈and 5₈. Locate 6 in the A column then locate the 5 in the B column. The point in 'sum' area where these two columns intersect is the 'sum' of two numbers.

68 + 58 = 138. 

Example − Addition

Octal Subtraction

The subtraction of octal numbers follows the same rules as the subtraction of numbers in any other number system. The only variation is in borrowed number. In the decimal system, you borrow a group of 10₁₀. In the binary system, you borrow a group of 2₁₀. In the octal system you borrow a group of 8₁₀.

Example − Subtraction

---

Binary Arithmetic

---

Binary arithmetic is essential part of all the digital computers and many other digital system.

Binary Addition

It is a key for binary subtraction, multiplication, division. There are four rules of binary addition.

In fourth case, a binary addition is creating a sum of (1 + 1 = 10) i.e. 0 is written in the given column and a carry of 1 over to the next column.

Example − Addition

Binary Subtraction

Subtraction and Borrow, these two words will be used very frequently for the binary subtraction. There are four rules of binary subtraction.

Example − Subtraction

Binary Multiplication

Binary multiplication is similar to decimal multiplication. It is simpler than decimal multiplication because only 0s and 1s are involved. There are four rules of binary multiplication.

Example − Multiplication

Binary Division

Binary division is similar to decimal division. It is called as the long division procedure.

Example − Division

Complement Arithmetic

---

Complements are used in the digital computers in order to simplify the subtraction operation and for the logical manipulations. For each radix-r system (radix r represents base of number system) there are two types of complements.

S.N.	Complement	Description
1	Radix Complement	The radix complement is referred to as the r's complement
2	Diminished Radix Complement	The diminished radix complement is referred to as the (r-1)'s complement

Binary system complements

As the binary system has base r = 2. So the two types of complements for the binary system are 2's complement and 1's complement.

1's complement

The 1's complement of a number is found by changing all 1's to 0's and all 0's to 1's. This is called as taking complement or 1's complement. Example of 1's Complement is as follows.

2's complement

The 2's complement of binary number is obtained by adding 1 to the Least Significant Bit (LSB) of 1's complement of the number.

2's complement = 1's complement + 1

Example of 2's Complement is as follows.

Codes Conversion

---

There are many methods or techniques which can be used to convert code from one format to another. We'll demonstrate here the following

• Binary to BCD Conversion
• BCD to Binary Conversion
• BCD to Excess-3
• Excess-3 to BCD

Binary to BCD Conversion

Steps

• Step 1 -- Convert the binary number to decimal.

• Step 2 -- Convert decimal number to BCD.

Example − convert (11101)₂ to BCD.

Step 1 − Convert to Decimal

Binary Number − 11101₂

Calculating Decimal Equivalent −

Step	Binary Number	Decimal Number
Step 1	111012	((1 × 24) + (1 × 23) + (1 × 22) + (0 × 21) + (1 × 20))10
Step 2	111012	(16 + 8 + 4 + 0 + 1)10
Step 3	111012	2910

Binary Number − 11101₂ = Decimal Number − 29₁₀

Step 2 − Convert to BCD

Decimal Number − 29₁₀

Calculating BCD Equivalent. Convert each digit into groups of four binary digits equivalent.

Step	Decimal Number	Conversion
Step 1	2910	00102 10012
Step 2	2910	00101001BCD

Result

(11101)2 = (00101001)BCD 

BCD to Binary Conversion

Steps

• Step 1 -- Convert the BCD number to decimal.

• Step 2 -- Convert decimal to binary.

Example − convert (00101001)_BCD to Binary.

Step 1 - Convert to BCD

BCD Number − (00101001)_BCD

Calculating Decimal Equivalent. Convert each four digit into a group and get decimal equivalent for each group.

Step	BCD Number	Conversion
Step 1	(00101001)BCD	00102 10012
Step 2	(00101001)BCD	210 910
Step 3	(00101001)BCD	2910

BCD Number − (00101001)_BCD = Decimal Number − 29₁₀

Step 2 - Convert to Binary

Used long division method for decimal to binary conversion.

Decimal Number − 29₁₀

Calculating Binary Equivalent −

Step	Operation	Result	Remainder
Step 1	29 / 2	14	1
Step 2	14 / 2	7	0
Step 3	7 / 2	3	1
Step 4	3 / 2	1	1
Step 5	1 / 2	0	1

As mentioned in Steps 2 and 4, the remainders have to be arranged in the reverse order so that the first remainder becomes the least significant digit (LSD) and the last remainder becomes the most significant digit (MSD).

Decimal Number − 29₁₀ = Binary Number − 11101₂

Result

(00101001)BCD = (11101)2 

BCD to Excess-3

Steps

• Step 1 -- Convert BCD to decimal.

• Step 2 -- Add (3)₁₀ to this decimal number.

• Step 3 -- Convert into binary to get excess-3 code.

Example − convert (1001)_BCD to Excess-3.

Step 1 − Convert to decimal

(1001)_BCD = 9₁₀

Step 2 − Add 3 to decimal

(9)₁₀ + (3)₁₀ = (12)₁₀

Step 3 − Convert to Excess-3

(12)₁₀ = (1100)₂

Result

(1001)BCD = (1100)XS-3 

Excess-3 to BCD Conversion

Steps

• Step 1 -- Subtract (0011)₂ from each 4 bit of excess-3 digit to obtain the corresponding BCD code.

Example − convert (10011010)_XS-3 to BCD.

Given XS-3 number = 1 0 0 1 1 0 1 0 Subtract (0011)2 = 0 0 1 1 0 0 1 1 -------------------- BCD = 0 1 1 0 0 1 1 1 

Result

(10011010)XS-3 = (01100111)BCD