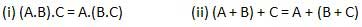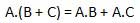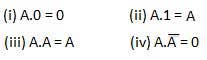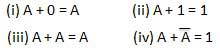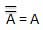Combinational Circuits

---

 

Combinational circuit is a circuit in which we combine the different gates in the circuit, for example encoder, decoder, multiplexer and demultiplexer. Some of the characteristics of combinational circuits are following −

• The output of combinational circuit at any instant of time, depends only on the levels present at input terminals.

• The combinational circuit do not use any memory. The previous state of input does not have any effect on the present state of the circuit.

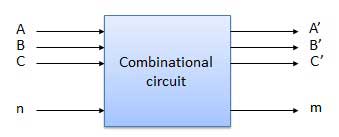
• A combinational circuit can have an n number of inputs and m number of outputs.

Block diagram

We're going to elaborate few important combinational circuits as follows.

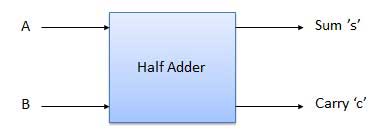
Half Adder

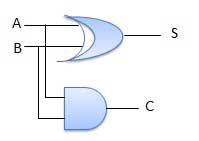
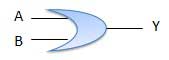
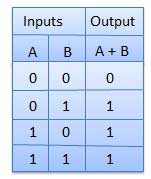
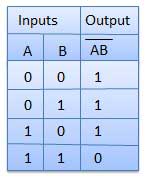
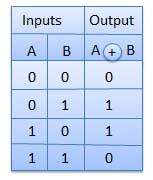
Half adder is a combinational logic circuit with two inputs and two outputs. The half adder circuit is designed to add two single bit binary number A and B. It is the basic building block for addition of two single bit numbers. This circuit has two outputs carry and sum.

Block diagram

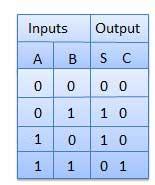
Truth Table

Circuit Diagram

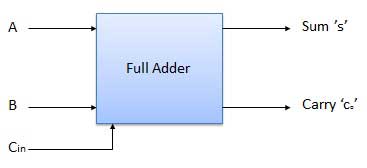
Full Adder

Full adder is developed to overcome the drawback of Half Adder circuit. It can add two one-bit numbers A and B, and carry c. The full adder is a three input and two output combinational circuit.

Block diagram

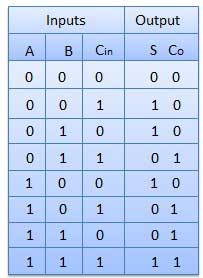
Truth Table

Circuit Diagram

N-Bit Parallel Adder

The Full Adder is capable of adding only two single digit binary number along with a carry input. But in practical we need to add binary numbers which are much longer than just one bit. To add two n-bit binary numbers we need to use the n-bit parallel adder. It uses a number of full adders in cascade. The carry output of the previous full adder is connected to carry input of the next full adder.

4 Bit Parallel Adder

In the block diagram, A₀ and B₀ represent the LSB of the four bit words A and B. Hence Full Adder-0 is the lowest stage. Hence its C_in has been permanently made 0. The rest of the connections are exactly same as those of n-bit parallel adder is shown in fig. The four bit parallel adder is a very common logic circuit.

Block diagram

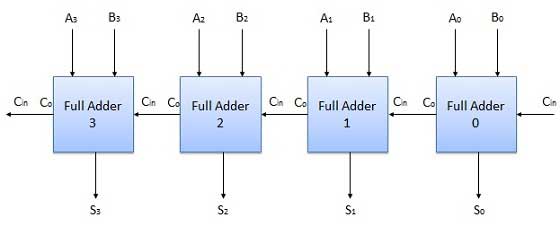
N-Bit Parallel Subtractor

The subtraction can be carried out by taking the 1's or 2's complement of the number to be subtracted. For example we can perform the subtraction (A-B) by adding either 1's or 2's complement of B to A. That means we can use a binary adder to perform the binary subtraction.

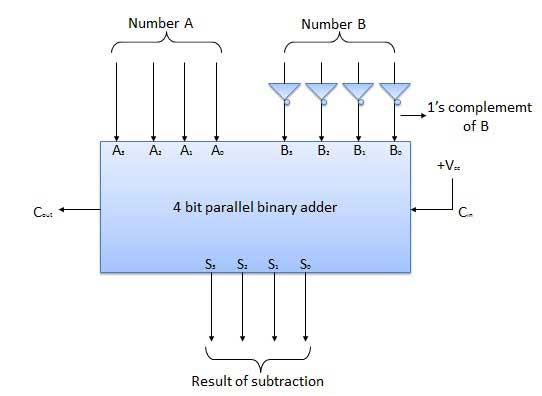
4 Bit Parallel Subtractor

The number to be subtracted (B) is first passed through inverters to obtain its 1's complement. The 4-bit adder then adds A and 2's complement of B to produce the subtraction. S₃ S₂ S₁ S₀ represents the result of binary subtraction (A-B) and carry output C_out represents the polarity of the result. If A > B then Cout = 0 and the result of binary form (A-B) then C_out = 1 and the result is in the 2's complement form.

Block diagram

Half Subtractors

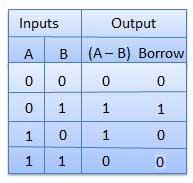
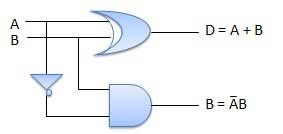
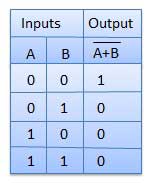
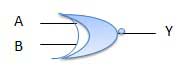
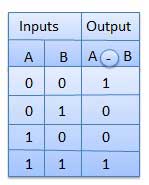
Half subtractor is a combination circuit with two inputs and two outputs (difference and borrow). It produces the difference between the two binary bits at the input and also produces an output (Borrow) to indicate if a 1 has been borrowed. In the subtraction (A-B), A is called as Minuend bit and B is called as Subtrahend bit.

Truth Table

Circuit Diagram

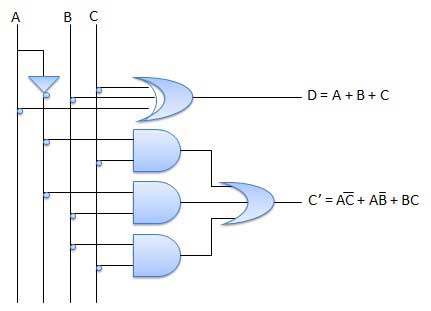
Full Subtractors

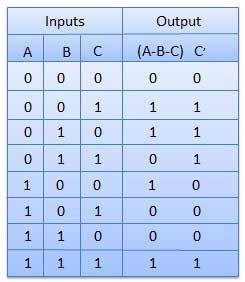
The disadvantage of a half subtractor is overcome by full subtractor. The full subtractor is a combinational circuit with three inputs A,B,C and two output D and C'. A is the 'minuend', B is 'subtrahend', C is the 'borrow' produced by the previous stage, D is the difference output and C' is the borrow output.

Truth Table

Circuit Diagram

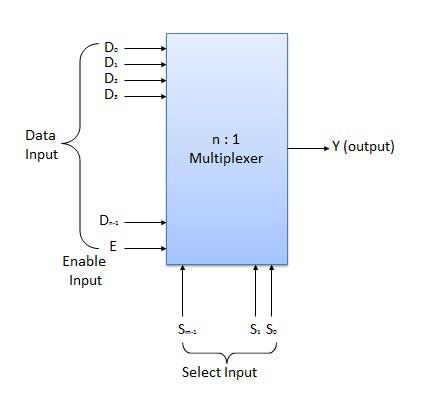
Multiplexers

Multiplexer is a special type of combinational circuit. There are n-data inputs, one output and m select inputs with 2m = n. It is a digital circuit which selects one of the n data inputs and routes it to the output. The selection of one of the n inputs is done by the selected inputs. Depending on the digital code applied at the selected inputs, one out of n data sources is selected and transmitted to the single output Y. E is called the strobe or enable input which is useful for the cascading. It is generally an active low terminal that means it will perform the required operation when it is low.

Block diagram

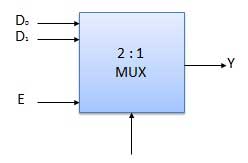
Multiplexers come in multiple variations

• 2 : 1 multiplexer
• 4 : 1 multiplexer
• 16 : 1 multiplexer
• 32 : 1 multiplexer

Block Diagram

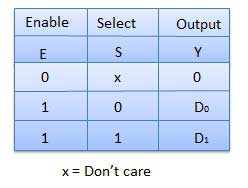
Truth Table

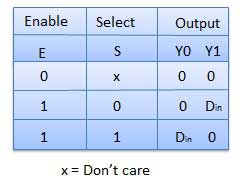
Demultiplexers

A demultiplexer performs the reverse operation of a multiplexer i.e. it receives one input and distributes it over several outputs. It has only one input, n outputs, m select input. At a time only one output line is selected by the select lines and the input is transmitted to the selected output line. A de-multiplexer is equivalent to a single pole multiple way switch as shown in fig.

Demultiplexers comes in multiple variations.

• 1 : 2 demultiplexer
• 1 : 4 demultiplexer
• 1 : 16 demultiplexer
• 1 : 32 demultiplexer

Block diagram

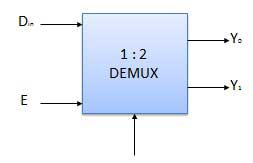
Truth Table

Decoder

A decoder is a combinational circuit. It has n input and to a maximum m = 2n outputs. Decoder is identical to a demultiplexer without any data input. It performs operations which are exactly opposite to those of an encoder.

Block diagram

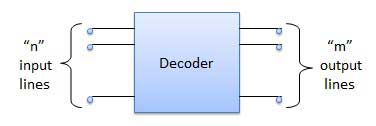
Examples of Decoders are following.

• Code converters
• BCD to seven segment decoders
• Nixie tube decoders
• Relay actuator

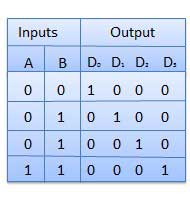
2 to 4 Line Decoder

The block diagram of 2 to 4 line decoder is shown in the fig. A and B are the two inputs where D through D are the four outputs. Truth table explains the operations of a decoder. It shows that each output is 1 for only a specific combination of inputs.

Block diagram

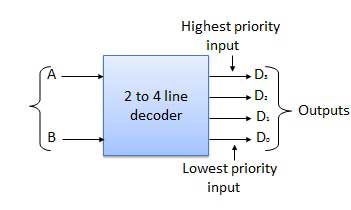
Truth Table

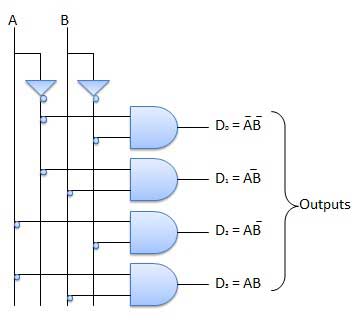
Logic Circuit

Encoder

Encoder is a combinational circuit which is designed to perform the inverse operation of the decoder. An encoder has n number of input lines and m number of output lines. An encoder produces an m bit binary code corresponding to the digital input number. The encoder accepts an n input digital word and converts it into an m bit another digital word.

Block diagram

Examples of Encoders are following.

• Priority encoders
• Decimal to BCD encoder
• Octal to binary encoder
• Hexadecimal to binary encoder

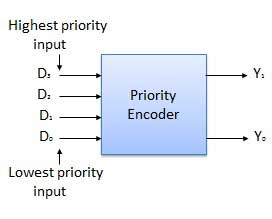
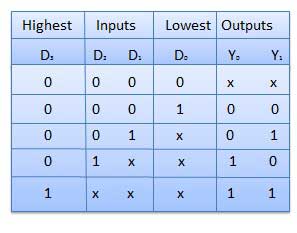
Priority Encoder

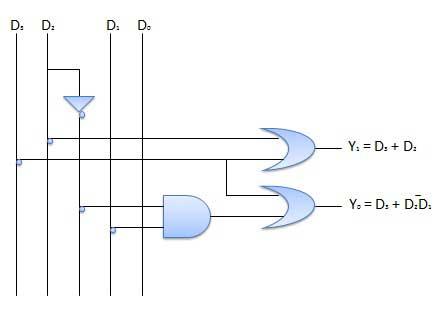
This is a special type of encoder. Priority is given to the input lines. If two or more input line are 1 at the same time, then the input line with highest priority will be considered. There are four input D₀, D₁, D₂, D₃ and two output Y₀, Y₁. Out of the four input D₃ has the highest priority and D₀ has the lowest priority. That means if D₃ = 1 then Y₁ Y₁ = 11 irrespective of the other inputs. Similarly if D₃ = 0 and D₂ = 1 then Y₁ Y₀ = 10 irrespective of the other inputs.

Block diagram

Truth Table

Logic Circuit

Logic Gates

---

Logic gates are the basic building blocks of any digital system. It is an electronic circuit having one or more than one input and only one output. The relationship between the input and the output is based on a certain logic. Based on this, logic gates are named as AND gate, OR gate, NOT gate etc.

AND Gate

A circuit which performs an AND operation is shown in figure. It has n input (n >= 2) and one output.

Logic diagram

Truth Table

OR Gate

A circuit which performs an OR operation is shown in figure. It has n input (n >= 2) and one output.

Logic diagram

Truth Table

NOT Gate

NOT gate is also known as Inverter. It has one input A and one output Y.

Logic diagram

Truth Table

NAND Gate

A NOT-AND operation is known as NAND operation. It has n input (n >= 2) and one output.

Logic diagram

Truth Table

NOR Gate

A NOT-OR operation is known as NOR operation. It has n input (n >= 2) and one output.

Logic diagram

Truth Table

XOR Gate

XOR or Ex-OR gate is a special type of gate. It can be used in the half adder, full adder and subtractor. The exclusive-OR gate is abbreviated as EX-OR gate or sometime as X-OR gate. It has n input (n >= 2) and one output.

Logic diagram

Truth Table

XNOR Gate

XNOR gate is a special type of gate. It can be used in the half adder, full adder and subtractor. The exclusive-NOR gate is abbreviated as EX-NOR gate or sometime as X-NOR gate. It has n input (n >= 2) and one output.

Logic diagram

Truth Table

Boolean Algebra

---

Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It uses only the binary numbers i.e. 0 and 1. It is also called as Binary Algebraor logical Algebra. Boolean algebra was invented by George Boole in 1854.

Rule in Boolean Algebra

Following are the important rules used in Boolean algebra.

• Variable used can have only two values. Binary 1 for HIGH and Binary 0 for LOW.

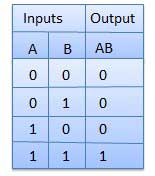
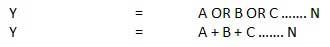
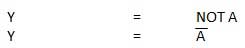
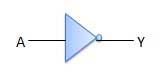
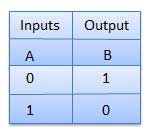
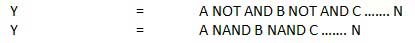
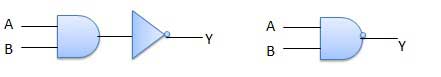
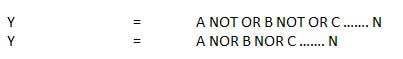
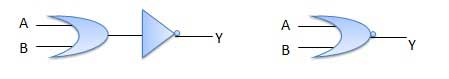
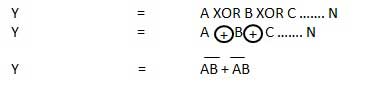
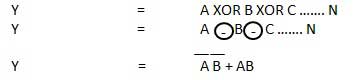
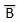• Complement of a variable is represented by an overbar (-). Thus, complement of variable B is represented as . Thus if B = 0 then = 1 and B = 1 then  = 0.

• ORing of the variables is represented by a plus (+) sign between them. For example ORing of A, B, C is represented as A + B + C.

• Logical ANDing of the two or more variable is represented by writing a dot between them such as A.B.C. Sometime the dot may be omitted like ABC.

Boolean Laws

There are six types of Boolean Laws.

Commutative law

Any binary operation which satisfies the following expression is referred to as commutative operation.

Commutative law states that changing the sequence of the variables does not have any effect on the output of a logic circuit.

Associative law

This law states that the order in which the logic operations are performed is irrelevant as their effect is the same.

Distributive law

Distributive law states the following condition.

AND law

These laws use the AND operation. Therefore they are called as AND laws.

OR law

These laws use the OR operation. Therefore they are called as OR laws.

INVERSION law

This law uses the NOT operation. The inversion law states that double inversion of a variable results in the original variable itself.

Important Boolean Theorems

Following are few important boolean Theorems.

Boolean function/theorems	Description
Boolean Functions	Boolean Functions and Expressions, K-Map and NAND Gates realization
De Morgan's Theorems	De Morgan's Theorem 1 and Theorem 2