Digital Counters

---

Counter is a sequential circuit. A digital circuit which is used for a counting pulses is known counter. Counter is the widest application of flip-flops. It is a group of flip-flops with a clock signal applied. Counters are of two types.

• Asynchronous or ripple counters.
• Synchronous counters.

Asynchronous or ripple counters

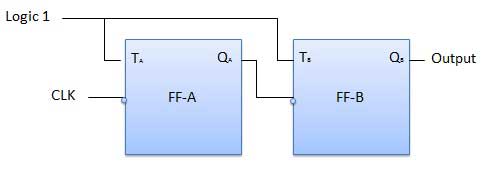
The logic diagram of a 2-bit ripple up counter is shown in figure. The toggle (T) flip-flop are being used. But we can use the JK flip-flop also with J and K connected permanently to logic 1. External clock is applied to the clock input of flip-flop A and Q_A output is applied to the clock input of the next flip-flop i.e. FF-B.

Logical Diagram

Operation

S.N.	Condition	Operation
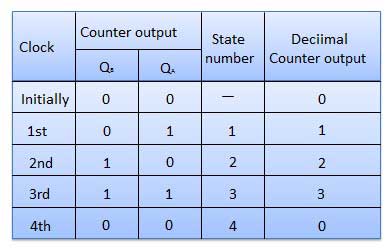
1	Initially let both the FFs be in the reset state	QBQA = 00 initially
2	After 1st negative clock edge	As soon as the first negative clock edge is applied, FF-A will toggle and QA will be equal to 1. QA is connected to clock input of FF-B. Since QA has changed from 0 to 1, it is treated as the positive clock edge by FF-B. There is no change in QB because FF-B is a negative edge triggered FF. QBQA = 01 after the first clock pulse.
3	After 2nd negative clock edge	On the arrival of second negative clock edge, FF-A toggles again and QA = 0. The change in QA acts as a negative clock edge for FF-B. So it will also toggle, and QBwill be 1. QBQA = 10 after the second clock pulse.
4	After 3rd negative clock edge	On the arrival of 3rd negative clock edge, FF-A toggles again and QA become 1 from 0. Since this is a positive going change, FF-B does not respond to it and remains inactive. So QB does not change and continues to be equal to 1. QBQA = 11 after the third clock pulse.
5	After 4th negative clock edge	On the arrival of 4th negative clock edge, FF-A toggles again and QA becomes 1 from 0. This negative change in QAacts as clock pulse for FF-B. Hence it toggles to change QBfrom 1 to 0. QBQA = 00 after the fourth clock pulse.

Truth Table

Synchronous counters

If the "clock" pulses are applied to all the flip-flops in a counter simultaneously, then such a counter is called as synchronous counter.

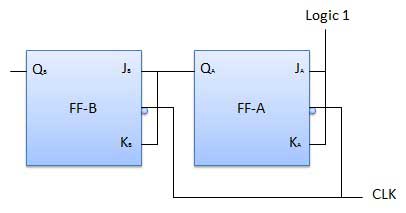
2-bit Synchronous up counter

The J_A and K_A inputs of FF-A are tied to logic 1. So FF-A will work as a toggle flip-flop. The J_B and K_B inputs are connected to Q_A.

Logical Diagram

Operation

S.N.	Condition	Operation
1	Initially let both the FFs be in the reset state	QBQA = 00 initially.
2	After 1st negative clock edge	As soon as the first negative clock edge is applied, FF-A will toggle and QA will change from 0 to 1. But at the instant of application of negative clock edge, QA , JB = KB = 0. Hence FF-B will not change its state. So QB will remain 0. QBQA = 01 after the first clock pulse.
3	After 2nd negative clock edge	On the arrival of second negative clock edge, FF-A toggles again and QA changes from 1 to 0. But at this instant QA was 1. So JB = KB= 1 and FF-B will toggle. Hence QB changes from 0 to 1. QBQA = 10 after the second clock pulse.
4	After 3rd negative clock edge	On application of the third falling clock edge, FF-A will toggle from 0 to 1 but there is no change of state for FF-B. QBQA = 11 after the third clock pulse.
5	After 4th negative clock edge	On application of the next clock pulse, QA will change from 1 to 0 as QB will also change from 1 to 0. QBQA = 00 after the fourth clock pulse.

Classification of counters

Depending on the way in which the counting progresses, the synchronous or asynchronous counters are classified as follows −

• Up counters
• Down counters
• Up/Down counters

UP/DOWN Counter

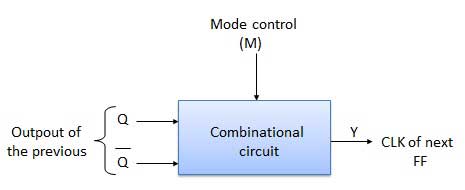
Up counter and down counter is combined together to obtain an UP/DOWN counter. A mode control (M) input is also provided to select either up or down mode. A combinational circuit is required to be designed and used between each pair of flip-flop in order to achieve the up/down operation.

• Type of up/down counters
• UP/DOWN ripple counters
• UP/DOWN synchronous counter

UP/DOWN Ripple Counters

In the UP/DOWN ripple counter all the FFs operate in the toggle mode. So either T flip-flops or JK flip-flops are to be used. The LSB flip-flop receives clock directly. But the clock to every other FF is obtained from (Q = Q bar) output of the previous FF.

• UP counting mode (M=0) − The Q output of the preceding FF is connected to the clock of the next stage if up counting is to be achieved. For this mode, the mode select input M is at logic 0 (M=0).

• DOWN counting mode (M=1) − If M = 1, then the Q bar output of the preceding FF is connected to the next FF. This will operate the counter in the counting mode.

Example

3-bit binary up/down ripple counter.

• 3-bit − hence three FFs are required.

• UP/DOWN − So a mode control input is essential.

• For a ripple up counter, the Q output of preceding FF is connected to the clock input of the next one.

• For a ripple up counter, the Q output of preceding FF is connected to the clock input of the next one.

• For a ripple down counter, the Q bar output of preceding FF is connected to the clock input of the next one.

• Let the selection of Q and Q bar output of the preceding FF be controlled by the mode control input M such that, If M = 0, UP counting. So connect Q to CLK. If M = 1, DOWN counting. So connect Q bar to CLK.

Block Diagram

Truth Table

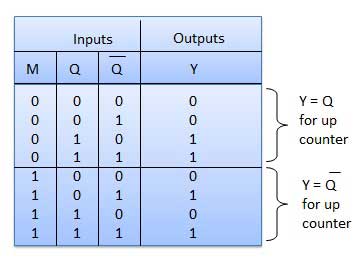
Operation

S.N.	Condition	Operation
1	Case 1 − With M = 0 (Up counting mode)	If M = 0 and M bar = 1, then the AND gates 1 and 3 in fig. will be enabled whereas the AND gates 2 and 4 will be disabled. Hence QA gets connected to the clock input of FF-B and QBgets connected to the clock input of FF-C. These connections are same as those for the normal up counter. Thus with M = 0 the circuit work as an up counter.
2	Case 2: With M = 1 (Down counting mode)	If M = 1, then AND gates 2 and 4 in fig. are enabled whereas the AND gates 1 and 3 are disabled. Hence QA bar gets connected to the clock input of FF-B and QB bar gets connected to the clock input of FF-C. These connections will produce a down counter. Thus with M = 1 the circuit works as a down counter.

Modulus Counter (MOD-N Counter)

The 2-bit ripple counter is called as MOD-4 counter and 3-bit ripple counter is called as MOD-8 counter. So in general, an n-bit ripple counter is called as modulo-N counter. Where, MOD number = 2ⁿ.

Type of modulus

• 2-bit up or down (MOD-4)
• 3-bit up or down (MOD-8)
• 4-bit up or down (MOD-16)

Application of counters

• Frequency counters
• Digital clock
• Time measurement
• A to D converter
• Frequency divider circuits
• Digital triangular wave generator.