Binary Codes

---

In the coding, when numbers, letters or words are represented by a specific group of symbols, it is said that the number, letter or word is being encoded. The group of symbols is called as a code. The digital data is represented, stored and transmitted as group of binary bits. This group is also called as binary code. The binary code is represented by the number as well as alphanumeric letter.

Advantages of Binary Code

Following is the list of advantages that binary code offers.

• Binary codes are suitable for the computer applications.

• Binary codes are suitable for the digital communications.

• Binary codes make the analysis and designing of digital circuits if we use the binary codes.

• Since only 0 & 1 are being used, implementation becomes easy.

Classification of binary codes

The codes are broadly categorized into following four categories.

• Weighted Codes
• Non-Weighted Codes
• Binary Coded Decimal Code
• Alphanumeric Codes
• Error Detecting Codes
• Error Correcting Codes

Weighted Codes

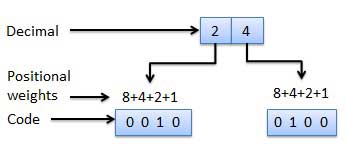
Weighted binary codes are those binary codes which obey the positional weight principle. Each position of the number represents a specific weight. Several systems of the codes are used to express the decimal digits 0 through 9. In these codes each decimal digit is represented by a group of four bits.

Non-Weighted Codes

In this type of binary codes, the positional weights are not assigned. The examples of non-weighted codes are Excess-3 code and Gray code.

Excess-3 code

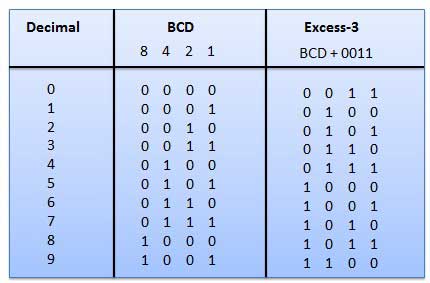
The Excess-3 code is also called as XS-3 code. It is non-weighted code used to express decimal numbers. The Excess-3 code words are derived from the 8421 BCD code words adding (0011)2 or (3)10 to each code word in 8421. The excess-3 codes are obtained as follows −

Example

Gray Code

It is the non-weighted code and it is not arithmetic codes. That means there are no specific weights assigned to the bit position. It has a very special feature that, only one bit will change each time the decimal number is incremented as shown in fig. As only one bit changes at a time, the gray code is called as a unit distance code. The gray code is a cyclic code. Gray code cannot be used for arithmetic operation.

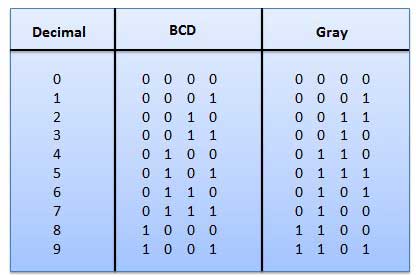
Application of Gray code

• Gray code is popularly used in the shaft position encoders.

• A shaft position encoder produces a code word which represents the angular position of the shaft.

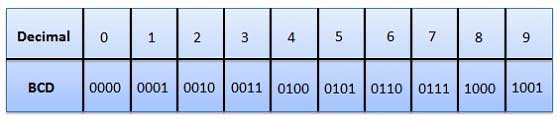
Binary Coded Decimal (BCD) code

In this code each decimal digit is represented by a 4-bit binary number. BCD is a way to express each of the decimal digits with a binary code. In the BCD, with four bits we can represent sixteen numbers (0000 to 1111). But in BCD code only first ten of these are used (0000 to 1001). The remaining six code combinations i.e. 1010 to 1111 are invalid in BCD.

Advantages of BCD Codes

• It is very similar to decimal system.
• We need to remember binary equivalent of decimal numbers 0 to 9 only.

Disadvantages of BCD Codes

• The addition and subtraction of BCD have different rules.

• The BCD arithmetic is little more complicated.

• BCD needs more number of bits than binary to represent the decimal number. So BCD is less efficient than binary.

Alphanumeric codes

A binary digit or bit can represent only two symbols as it has only two states '0' or '1'. But this is not enough for communication between two computers because there we need many more symbols for communication. These symbols are required to represent 26 alphabets with capital and small letters, numbers from 0 to 9, punctuation marks and other symbols.

The alphanumeric codes are the codes that represent numbers and alphabetic characters. Mostly such codes also represent other characters such as symbol and various instructions necessary for conveying information. An alphanumeric code should at least represent 10 digits and 26 letters of alphabet i.e. total 36 items. The following three alphanumeric codes are very commonly used for the data representation.

• American Standard Code for Information Interchange (ASCII).
• Extended Binary Coded Decimal Interchange Code (EBCDIC).
• Five bit Baudot Code.

ASCII code is a 7-bit code whereas EBCDIC is an 8-bit code. ASCII code is more commonly used worldwide while EBCDIC is used primarily in large IBM computers.

Error Codes

There are binary code techniques available to detect and correct data during data transmission.

Error Code	Description
Error Detection and Correction	Error de

Number System Conversion

---

There are many methods or techniques which can be used to convert numbers from one base to another. We'll demonstrate here the following −

• Decimal to Other Base System
• Other Base System to Decimal
• Other Base System to Non-Decimal
• Shortcut method − Binary to Octal
• Shortcut method − Octal to Binary
• Shortcut method − Binary to Hexadecimal
• Shortcut method − Hexadecimal to Binary

Decimal to Other Base System

Steps

• Step 1 − Divide the decimal number to be converted by the value of the new base.

• Step 2 − Get the remainder from Step 1 as the rightmost digit (least significant digit) of new base number.

• Step 3 − Divide the quotient of the previous divide by the new base.

• Step 4 − Record the remainder from Step 3 as the next digit (to the left) of the new base number.

Repeat Steps 3 and 4, getting remainders from right to left, until the quotient becomes zero in Step 3.

The last remainder thus obtained will be the Most Significant Digit (MSD) of the new base number.

Example −

Decimal Number: 29₁₀

Calculating Binary Equivalent −

Step	Operation	Result	Remainder
Step 1	29 / 2	14	1
Step 2	14 / 2	7	0
Step 3	7 / 2	3	1
Step 4	3 / 2	1	1
Step 5	1 / 2	0	1

As mentioned in Steps 2 and 4, the remainders have to be arranged in the reverse order so that the first remainder becomes the Least Significant Digit (LSD) and the last remainder becomes the Most Significant Digit (MSD).

Decimal Number − 29₁₀ = Binary Number − 11101₂.

Other Base System to Decimal System

Steps

• Step 1 − Determine the column (positional) value of each digit (this depends on the position of the digit and the base of the number system).

• Step 2 − Multiply the obtained column values (in Step 1) by the digits in the corresponding columns.

• Step 3 − Sum the products calculated in Step 2. The total is the equivalent value in decimal.

Example

Binary Number − 11101₂

Calculating Decimal Equivalent −

Step	Binary Number	Decimal Number
Step 1	111012	((1 × 24) + (1 × 23) + (1 × 22) + (0 × 21) + (1 × 20))10
Step 2	111012	(16 + 8 + 4 + 0 + 1)10
Step 3	111012	2910

Binary Number − 11101₂ = Decimal Number − 29₁₀

Other Base System to Non-Decimal System

Steps

• Step 1 − Convert the original number to a decimal number (base 10).

• Step 2 − Convert the decimal number so obtained to the new base number.

Example

Octal Number − 25₈

Calculating Binary Equivalent −

Step 1 − Convert to Decimal

Step	Octal Number	Decimal Number
Step 1	258	((2 × 81) + (5 × 80))10
Step 2	258	(16 + 5 )10
Step 3	258	2110

Octal Number − 25₈ = Decimal Number − 21₁₀

Step 2 − Convert Decimal to Binary

Step	Operation	Result	Remainder
Step 1	21 / 2	10	1
Step 2	10 / 2	5	0
Step 3	5 / 2	2	1
Step 4	2 / 2	1	0
Step 5	1 / 2	0	1

Decimal Number − 21₁₀ = Binary Number − 10101₂

Octal Number − 25₈ = Binary Number − 10101₂

Shortcut method - Binary to Octal

Steps

• Step 1 − Divide the binary digits into groups of three (starting from the right).

• Step 2 − Convert each group of three binary digits to one octal digit.

Example

Binary Number − 10101₂

Calculating Octal Equivalent −

Step	Binary Number	Octal Number
Step 1	101012	010 101
Step 2	101012	28 58
Step 3	101012	258

Binary Number − 10101₂ = Octal Number − 25₈

Shortcut method - Octal to Binary

Steps

• Step 1 − Convert each octal digit to a 3 digit binary number (the octal digits may be treated as decimal for this conversion).

• Step 2 − Combine all the resulting binary groups (of 3 digits each) into a single binary number.

Example

Octal Number − 25₈

Calculating Binary Equivalent −

Step	Octal Number	Binary Number
Step 1	258	210 510
Step 2	258	0102 1012
Step 3	258	0101012

Octal Number − 25₈ = Binary Number − 10101₂

Shortcut method - Binary to Hexadecimal

Steps

• Step 1 − Divide the binary digits into groups of four (starting from the right).

• Step 2 − Convert each group of four binary digits to one hexadecimal symbol.

Example

Binary Number − 10101₂

Calculating hexadecimal Equivalent −

Step	Binary Number	Hexadecimal Number
Step 1	101012	0001 0101
Step 2	101012	110 510
Step 3	101012	1516

Binary Number − 10101₂ = Hexadecimal Number − 15₁₆

Shortcut method - Hexadecimal to Binary

Steps

• Step 1 − Convert each hexadecimal digit to a 4 digit binary number (the hexadecimal digits may be treated as decimal for this conversion).

• Step 2 − Combine all the resulting binary groups (of 4 digits each) into a single binary number.

Example

Hexadecimal Number − 15₁₆

Calculating Binary Equivalent −

Step	Hexadecimal Number	Binary Number
Step 1	1516	110 510
Step 2	1516	00012 01012
Step 3	1516	000101012

Hexadecimal Number − 15₁₆ = Binary Number − 10101₂

Digital Number System

---

A digital system can understand positional number system only where there are a few symbols called digits and these symbols represent different values depending on the position they occupy in the number.

A value of each digit in a number can be determined using

• The digit

• The position of the digit in the number

• The base of the number system (where base is defined as the total number of digits available in the number system).

Decimal Number System

The number system that we use in our day-to-day life is the decimal number system. Decimal number system has base 10 as it uses 10 digits from 0 to 9. In decimal number system, the successive positions to the left of the decimal point represents units, tens, hundreds, thousands and so on.

Each position represents a specific power of the base (10). For example, the decimal number 1234 consists of the digit 4 in the units position, 3 in the tens position, 2 in the hundreds position, and 1 in the thousands position, and its value can be written as

(1×1000) + (2×100) + (3×10) + (4×l) (1×103) + (2×102) + (3×101) + (4×l00) 1000 + 200 + 30 + 1 1234 

As a computer programmer or an IT professional, you should understand the following number systems which are frequently used in computers.

S.N.	Number System & Description
1	Binary Number System Base 2. Digits used: 0, 1
2	Octal Number System Base 8. Digits used: 0 to 7
3	Hexa Decimal Number System Base 16. Digits used: 0 to 9, Letters used: A- F

Binary Number System

Characteristics

• Uses two digits, 0 and 1.

• Also called base 2 number system

• Each position in a binary number represents a 0 power of the base (2). Example: 2⁰

• Last position in a binary number represents an x power of the base (2). Example: 2^x where x represents the last position - 1.

Example

Binary Number: 10101₂

Calculating Decimal Equivalent −

Step	Binary Number	Decimal Number
Step 1	101012	((1 × 24) + (0 × 23) + (1 × 22) + (0 × 21) + (1 × 20))10
Step 2	101012	(16 + 0 + 4 + 0 + 1)10
Step 3	101012	2110

Note: 10101₂ is normally written as 10101.

Octal Number System

Characteristics

• Uses eight digits, 0,1,2,3,4,5,6,7.

• Also called base 8 number system

• Each position in an octal number represents a 0 power of the base (8). Example: 8⁰

• Last position in an octal number represents an x power of the base (8). Example: 8^x where x represents the last position - 1.

Example

Octal Number − 12570₈

Calculating Decimal Equivalent −

Step	Octal Number	Decimal Number
Step 1	125708	((1 × 84) + (2 × 83) + (5 × 82) + (7 × 81) + (0 × 80))10
Step 2	125708	(4096 + 1024 + 320 + 56 + 0)10
Step 3	125708	549610

Note: 12570₈ is normally written as 12570.

Hexadecimal Number System

Characteristics

• Uses 10 digits and 6 letters, 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.

• Letters represents numbers starting from 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.

• Also called base 16 number system.

• Each position in a hexadecimal number represents a 0 power of the base (16). Example 16⁰.

• Last position in a hexadecimal number represents an x power of the base (16). Example 16^x where x represents the last position - 1.

Example −

Hexadecimal Number: 19FDE₁₆

Calculating Decimal Equivalent −

Step	Hexadecimal Number	Decimal Number
Step 1	19FDE16	((1 × 164) + (9 × 163) + (F × 162) + (D × 161) + (E × 160))10
Step 2	19FDE16	((1 × 164) + (9 × 163) + (15 × 162) + (13 × 161) + (14 × 160))10
Step 3	19FDE16	(65536 + 36864 + 3840 + 208 + 14)10
Step 4	19FDE16	10646210

Note − 19FDE₁₆ is normally written as 19FDE.

Overview

---

In the modern world of electronics, the term Digital is generally associated with a computer because the term Digital is derived from the way computers perform operation, by counting digits. For many years, the application of digital electronics was only in the computer system. But now-a-days, digital electronics is used in many other applications. Following are some of the examples in which Digital electronics is heavily used.

• Industrial process control
• Military system
• Television
• Communication system
• Medical equipment
• Radar
• Navigation

Signal

Signal can be defined as a physical quantity, which contains some information. It is a function of one or more than one independent variables. Signals are of two types.

• Analog Signal
• Digital Signal

Analog Signal

An analog signal is defined as the signal having continuous values. Analog signal can have infinite number of different values. In real world scenario, most of the things observed in nature are analog. Examples of the analog signals are following.

• Temperature
• Pressure
• Distance
• Sound
• Voltage
• Current
• Power

Graphical representation of Analog Signal (Temperature)

The circuits that process the analog signals are called as analog circuits or system. Examples of the analog system are following.

• Filter
• Amplifiers
• Television receiver
• Motor speed controller

Disadvantage of Analog Systems

• Less accuracy
• Less versatility
• More noise effect
• More distortion
• More effect of weather

Digital Signal

A digital signal is defined as the signal which has only a finite number of distinct values. Digital signals are not continuous signals. In the digital electronic calculator, the input is given with the help of switches. This input is converted into electrical signal which have two discrete values or levels. One of these may be called low level and another is called high level. The signal will always be one of the two levels. This type of signal is called digital signal. Examples of the digital signal are following.

• Binary Signal
• Octal Signal
• Hexadecimal Signal

Graphical representation of the Digital Signal (Binary)

The circuits that process the digital signals are called digital systems or digital circuits. Examples of the digital systems are following.

• Registers
• Flip-flop
• Counters
• Microprocessors

Advantage of Digital Systems

• More accuracy
• More versatility
• Less distortion
• Easy communicate
• Possible storage of information

Comparison of Analog and Digital Signal

S.N.	Analog Signal	Digital Signal
1	Analog signal has infinite values.	Digital signal has a finite number of values.
2	Analog signal has a continuous nature.	Digital signal has a discrete nature.
3	Analog signal is generated by transducers and signal generators.	Digital signal is generated by A to D converter.
4	Example of analog signal − sine wave, triangular waves.	Example of digital signal − binary signal.

Shortcut Keys

---

Short-cut keys Functions
Commonly Used Short-cut Keys
F1	Universal help (for any sort of program).
Alt + F	File menu options in current program.
Alt + E	Edits options in current program.
Ctrl + A	Selects all text.
Ctrl + X	Cuts the selected item.
Ctrl + C	Copies the selected item.
Ctrl + V	Pastes copied item.
Home	Takes the user to the beginning of the current line.
End	Takes the user to the end of the current line.
Ctrl + Home	Takes the user to the beginning of the document.
Ctrl + End	Takes the user to the end of the document.
Shift + Home	Highlights from the current place to the beginning of line.
Shift + End	Highlights from the current place to the end of line.
Microsoft Windows Shortcut Keys
Ctrl + F4	Closes window in program.
Alt + F4	Closes current open program.
F2	Renames the selected icon.
F3	Start find from desktop.
F4	Opens the drive selection when browsing.
F5	Refreshes contents.
Alt + Tab	Switches from one open application to another open application.
Alt + Shift + Tab	Switches backwards between open applications.
Alt + Print Screen	Creates screen shot for current program.
Ctrl + Alt + Del.	Opens windows task manager/reboot.
Ctrl + Esc	Brings up start menu.
Alt + Esc	Switches between applications on taskbar.
Ctrl + Plus (+) Key	Automatically adjusts widths of all columns in Windows Explorer.
Alt + Enter	Opens properties window of selected icon or program.
Shift + F10	Simulates right-click on selected item.
Shift + Del	Deletes selected programs/files permanently.
Holding Shift During Boot-up	Enables boot safe mode or bypass system files.
Ctrl + N	Starts a new note.
Ctrl + O	Opens a recently used note.
Ctrl + S	Saves changes to a note.
Ctrl + P	Prints a note.
Alt + F4	Closes a note and its Journal window.
Ctrl + Z	Helps Undo a change.
Ctrl + Y	Helps Redo a change.
Ctrl + A	Selects all items on a page.
Ctrl + X	Cuts a selection.
Ctrl + C	Copies a selection to the Clipboard.
Ctrl + V	Pastes a selection from the Clipboard.
Esc	Cancels a selection.
Ctrl + F	Start a search tool.
Ctrl + Shift + C	Display a shortcut menu for column headings in a note list.
Microsoft Word Shortcut Keys
Ctrl + N	Creates a new document.
Ctrl + O	Opens an existing document.
Ctrl + S	Saves changes to a document.
F12	Saves the document as a new file.
Ctrl + P	Prints a document.
Ctrl + Z	Helps Undo a change.
Ctrl + Y	Helps Redo a change.
Ctrl + A	Selects the whole document.
Ctrl + X	Helps cut a selection
Ctrl + C	Copies a selection to the Clipboard.
Ctrl + V	Pastes a selection from the Clipboard.
Ctrl + B	Makes selected text bold.
Ctrl + I	Italicizes selected text.
Ctrl + U	Underlines selected texts.
Ctrl + L	Aligns text left.
Ctrl + R	Aligns text right.
Ctrl + E	Aligns text center.
Ctrl + J	Helps justify text.
Ctrl + 1	Sets single line spacing.
Ctrl + 2	Sets double line spacing.
Ctrl + 5	Sets line spacing to 1.5.
Ctrl + Shift + A	Changes characters to all capitals.
Ctrl + D	Inserts a Microsoft Paint drawing.
Ctrl + F	Finds text
Ctrl + Home	Moves to the beginning of the document.
Ctrl + End	Moves to the end of the document.

Development

---

In this chapter, we will discuss the development in Computer Science chronologically.

The following table lists down the development −

Year	Development
1959	Transistors: IBM 7090; IBM 1401
1962	NPN transistor
1963	Mouse; CMOS patented
1964	CDC 6600; IBM Data Cell Drive
1966	Integrated circuits: HP 2116A
1966	Apollo Guidance Computer
1969	Honeywell 316
1971	8" floppy disk; ILLIAC IV
1973	Micral first microprocessor PC
1980	Sinclair ZX80, Seagate hard disk drive
1981	IBM PC, Acorn BBC Micro
1983	Apple Lisa; 3.5" floppy
1984	Apple Mac; Apple Lisa 2
1988	Dell
1989	NeXT
1991	Apple Switches to PowerPC
1992	HP 95LX; Palmtop PC
1995	IBM Deep Blue chess computer
1996	USB 1.0
1997	Compaq buys Tandem; CD-RW
1998	iMac
2000	USB 2
2001	Apple iPod
2005	Mac Mini
2006	Apple transition to Intel
2007	iPhone 1
2008	USB 3.0
2010	Apple iPad
2012	IBM zEnterprise System

Abbreviations

---

In this chapter, we will discuss the different abbreviations in Computer Science. The following table lists down those abbreviations −

Abbreviation	Full-name
A/D	Analog-to-Digital
ABC	Atanasoff Berry Computer
ACM	Association for Computing Machinery
AI	Artificial Intelligence
ALGOL	Algorithic Language
ALU	Arithmetic Logic Unit
AMD	Advanced Micro Devices
APRANET	Advanced Research Project Agency Network
ASCII	American Standard Code for Information Interchange
BASIC	Beginners All-purpose Symbolic Instruction Code
BCD	Binary Coded Decimal
BIOS	Basic Inpute Output System
BIPS	Billions of Instructions Per Second
BPI	Bytes Per Inch
CAD	Computer Aided Design
CAE	Computer Aided Engineering
CAN	Campus Area Network
CASE	Computer Aided Software Engineering
CD	Compact Disk
CDC	Control Data Corporation
CD-R	CD-Recordable
CD-ROM	Compact Disk Read Only Memory
CD-RW	CD Read/Write
CL	Command Language
CLI	Command Line Interface
COBOL	Common Business Oriented
CODASYL	Conference On Data Systems
CPU	Central Processing Unit
CRT	Cathode Ray Tube
D/A	Digital-to-Analog
DAT	Digital Audio Tape
DBMS	Data Base Management System
DBS	Demand Based Switching
DDL	Data Definition Language
DDS	Digital Data Storage
DEC	Digital Equipment Corporation
DMA	Direct Memory Access
DNA	Digital Network Architecture
DPI	Dots Per Inch
DRAM	Dynamic RAM
DSN	Distributed Systems Network
DTS	Digital Theater System
DVD	Digital Video/Versatile Disk
EBCDIC	Extended Binary Coded Decimal Interchange Code
EDSAC	Electronic Delay Storage Automatic Calculator
EDVAC	Electronic Discrete Variable Automatic Calculator
EFM	Eight-to-Fourteen Modulation
ENIAC	Electronic Numerical Integrator And Calculator
EPG	Electronic Programming Guide
EPIC	Explicitly Parallel Instruction Computing
EPROM	Erasable Programmable Read-Only Memory
FAT	File Allocation Table
FDM	Frequency Division Multiplexing
FEP	Front End Processor
FLOPS	Floating Point Operations Per Second
FM	Frequency Modulation
FMS	File Management System
FORTRAN	FORmula TRANslation
FSK	Frequency Shift Keying
FTP	File Transfer Protocol
GB	Giga Bytes
GFLOPS	Giga FLOPS
GHz	Giga Hertz
GNU	Gnu Not Unix
GPRS	General Packet Radio Service
GSM	Global System for Mobile communication
GUI	Graphical User Interface
HP	Hewlett Packard
HSS	Hierarchical Storage System
HTML	HyperText Markup Language
HTTP	HyperText Transport Protocol
IBM	International Business Machine
IC	Integrated Circuit
IDN	Integrated Digital Networks
IP	Internet Protocol
IrDA	Infrared Data Association
ISDN	Integrated Services Digital Network
ISP	Internet Service Provider
JPEG	Joint Photographic Experts Group
JRE	Java Runtime Engine
JSP	Java Server Pages
KB	Kilo Bytes
KHz	Kilo Hertz
LAN	Local Area Network
LCD	Liquid Crystal Display
LED	Light Emitting Diode
LPM	Line Per Minute
LSI	Large Scael Integration
MAN	Metropolitan Area Network
MAR	Memory Address Register
MB	Mega Bytes
MBR	Memory Buffer Register
MHz	Mega Hertz
MIDI	Musical Instrument Digital Interface
MIPS	Millions of Instructions Per Second
MNP	Microcom Network Protocol
MPEG	Moving Pictures Experts Group
MS-DOS	MicroSoft Disk Operating System
MVT	Multiprogramming with Variable Tasks
NIC	Network Interface Card
NICNET	National Informatics Center NETwork
NOS	Network Operating System
OCR	Optical Character Recognition
OMR	Optical Mark Reader
OS	Operating System
OSI	Open System Interconnection
OSS	Open Source Software
PAN	Personal Area Network
PC	Personal Computer
PDF	Portable Document Format
PDL	Program Design Language
PDP	Program Data Processor
PIP	Peripheral Interchange Program
PROM	Programmable Read-Only Memory
QoS	Quality of Service
RAM	Random Access Memory
ROM	Read Only Memory
SDLC	Software Development Life Cycle
SEQUEL	Structured English QUEry Language
SGML	Syntax for Generalized Markup Language
SIMM	Single In-line Memory Module
SNA	Systems Network Architecture
SNOBOL	StriNg Oriented and symBOlic Language
SQL	Structured Query Language
SRAM	Static RAM
SSI	Small Scale Integration
TB	Tera Bytes
TCP	Transport Control Protocol
TDM	Time Division Multiplexing
UDP	User Datagram Protocol
ULSI	Ultra Large Scale Integration
UPC	Universal Product Code
URL	Uniform Resource Locator
USB	Universal Serial Bus
UTF	Unicode Transformation Format
VAN	Value Added Network
VCR	Video Cassette Recorder
VDT	Video Display Terminal
VGA	Video Graphics Array
VOD	Video-On-Demand
VoIP	Voice over Internet Protocol
VSAT	Very Small Aperture Terminal
WAN	Wide Area Network
WAP	Wireless Application Protocol
WiMAX	Worldwide Interoperability for Microwave Access
WLAN	Wireless Local Area Network
WLL	Wireless Local Loop
WORM	Write Once Read Many
WWW	World Wide Web
XHTML	eXtensible HyperText Markup Language
XML	eXtensible Markup Language
X.400	Electronic Mail Protocol
X.500	Directory Server Protocol